
ハワード・マークスさんの「投資で一番大切な20の教え」にあった、
「経験豊富な投資家がいる。大胆不敵な投資家がいる。しかし、経験豊富で大胆不敵な投資家はいない。」
という投資格言がグサッときました。
これは即ち、リスクを取りすぎた投資家は長くは生き残れないということです。
また、仮に運よく儲かっても、だから正しい判断をしたとは言えず、なぜなら未来は未知なのだから、良い決断とはそれを下した時に最適だったものであり、決断が正しかったのかどうかを結果から判断することはできないとのことでした。
「投資は結果が全て。」
なんとなくこんな言葉を鵜呑みにしてきましたが、ある面ではそれが正しくとも、他の面では間違えているのかも知れません。
破産の可能性の高いようなリスクテイクは、仮に運よく一時的にはハイリターンを得られたとしても、他の未来では、もしくは長期的には、破産するのが必然なのかも知れません。
もしくは、大きなリスクテイクをするなら、少なくともタイミングには細心の注意を払う必要があるのだとも言えそうです。
景気サイクルとセクターETFの関係性
https://www.yutainvest.com/business-cycle-and-stock-picking-in-may-2021/
タイミングなんてさっぱりわかりません。むしろタイミング売買は長期的には利益を減らすことすら知られています。とは言え、そんなTochiにでもなんとなくわかるのは、リスクを取るべきタイミングは今じゃないこと。利上げとインフレとQTと逆イールドの、今じゃないこと・・。
まあ、時既に遅しです。ガッツリとハイリスクのレバ3倍ETF(TQQQ、FAS)を握っています。
今思えば年間200万円も稼げれば十分だったハズなので、そもそもこんな過剰なリスクは無用だった様にも思えます。どうやらリターンのみに目がくらみ、血が登り、リスクを軽視しすぎていた様です。
でも、リスクって一体何だろう?
損切りしないのに変動のリスクなんて恐れる必要がどこにあるのだろう?
そんな不思議なリスクに関して、気になった記事を2つ貼り付けます。
S&P500のリターンの中央値はレバレッジ1.75倍が最適!
1つ目はチャンドラさんの「社畜がインデックス投資で資産を築く」ブログです。
感覚とは合致しませんが、投資の世界では一般にリスク=標準偏差(平均からのゆらぎの大きさ)と捉えるようです。
レバレッジ比率(L)と平均値・中央値の関係(*リターン7%, 標準偏差20%として)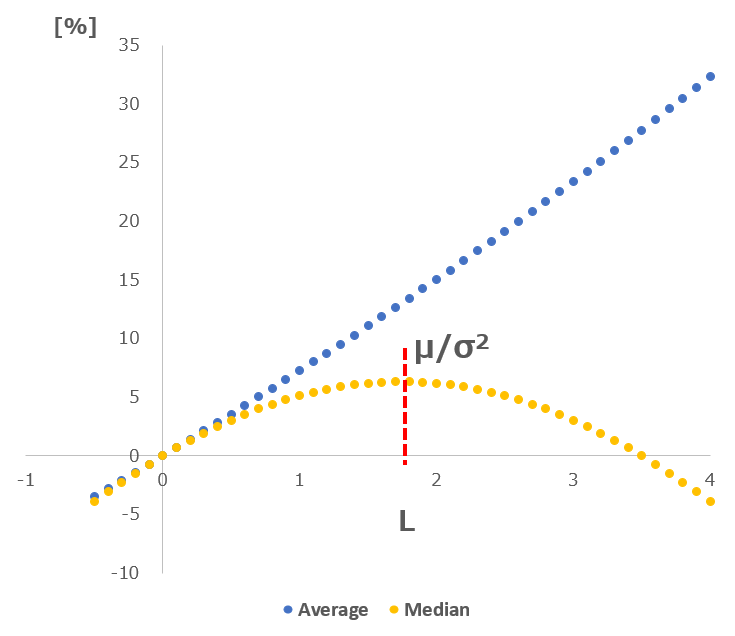
https://chandraroom.com/modern-portfolio-stock-leverage
最大値は、μ(リターン)/σ(標準偏差)^2=1.75。
リターンの平均がプラスならば、レバレッジが高くなるほど平均リターンも高くになるものの、中央値には(リターンと標準偏差に応じた)特定のピークがあるとのこと。
今一イメージがわきませんでしたが、次のグラフを見て何となく腑に落ちました。
レバレッジによるリターンの確率分布の時間変化(*リターン7%, 標準偏差20%として)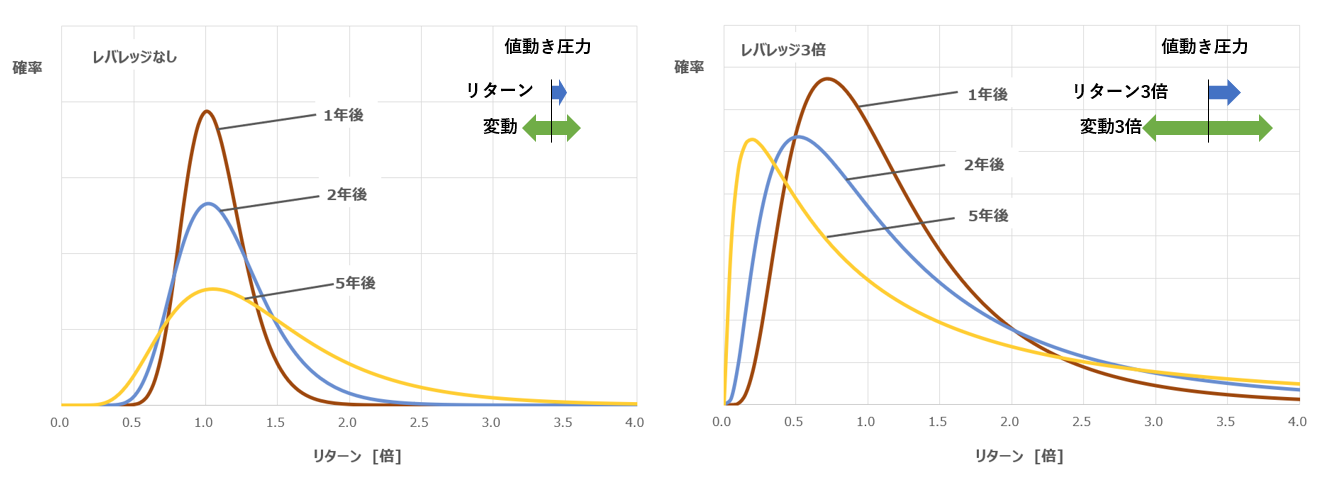
https://chandraroom.com/levergare-3rd-ganponware
年数が経過した場合、リターンがどの様な分布になるかを示したグラフですが、レバレッジ3倍の方(右側)は経年でリターン1.0倍を下回るエリアの面積(確率)がレバレッジ1倍(左側)と比べて広くなっています。
リターンも変動も同じ3倍なのにおかしい様な気がしますが、これはリターン1.0倍から左側のエリアが狭い(0~1倍)のに対し、右側のエリアは広い(1~∞倍)ことが要因だと考えられます。
例えば、無限に広い部屋であればホコリは均一に積もりますが、狭い部屋ではホコリの動きが制限される壁際により多く積もるのと同じです(たぶん)。もしくは、ギャンブルをやり続けるとお財布の中身には限りがあるので、多くの人が破産するのと同じです 😱
時間の経過で部屋の隅に溜まるホコリのシミュレーション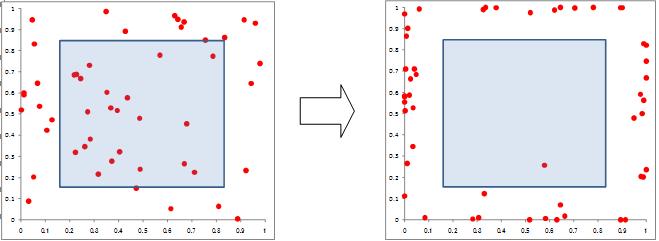
https://sci.tea-nifty.com/blog/2011/02/excel-vba-ce3c.html
よって、博打感覚であればレバレッジは何倍でもOKですが、長期投資として考えるならば、S&P500の場合は2倍程度が妥当だと言えそうです。
ちなみに、QQQの場合は8倍程度が妥当だそうです(過去10年の標準偏差15.32%, リターン19.05%として)。なお、最適倍率は将来のリターンと標準偏差によって大きく変動し、標準偏差の影響をより強く受けます。
https://chandraroom.com/tecl-tqqq-leverage
経費や金利を考慮すると1.92倍が最適!
2つ目はカガミルさんの「東大卒医師の投資と子育て」ブログです。
こちらは隠れコストを含めると2%を超えるレバレッジETFの手数料及び金利を含めた計算とのことなので、より現実に近い値だと思われます。
リターンを最大化するレバレッジ比率
https://kagamiru.com/max-return-leverage/
計算がさっぱりわかりませんでしたが、チャンドラさんとほぼ同じくS&P500の場合は2倍程度のレバレッジが妥当という結論になっています。金利や経費を考慮すると最適レバレッジがわずかに低下するようです。
しかし、金利や経費を無視するならば、リターンはレバレッジに比例しそうなものですが、何故かチャンドラさんの中央値を最大化する式と非常に似た式になっています(*ガンマ; γは、例えば年利7%の場合、log(1.07)=0.0676…と換算する)。
よく解りませんが、もしかするとここで使われているリターンの意味は、平均リターンではなく、リターンの中央値ということなのかも知れません・・(わからん!)。
例えば…)リターン10%、標準偏差20%の場合
・中央値を最大化するレバレッジ比率=0.1/0.2/0.2=2.5倍
・最適レバレッジ比率(金利や経費を無視)=0.5+log(1.1)/0.2/0.2=0.5+0.09531/0.2/0.2=0.5+2.38275≒2.9倍
くっ、微妙に違う!
自然対数 loge(x)計算機

まあなんにせよ、レバレッジは控え目がイーラシーー!


コメント